Thursday, March 27, 2008
Tuesday, March 25, 2008
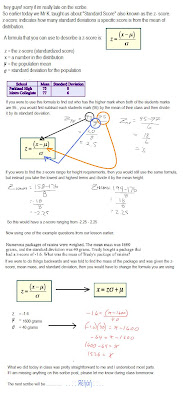
Find the percent of z-scores in a normal standard distribution that are:
a) below z = 0.52
Now to figure this out normally you would press 2nd [vars] and then you would go to the DRAW menu. ShadeNorm is the first function in the menu. After pressing ShadeNorm in the bracets you would enter -5, 0.52. Remember the smallest number is to be entered first. And the reason why you enter -5 is because the curve continues on past the -4 mark for the normal bell shaped curve. So when finished your answer should look like so.
ShadeNorm( -5, 0.52) = 0.6985
Now the new function that we learned today is the commulitive distribution function.
To find this on your calculator you would press 2nd [vars] and its the 2nd function in the menu. It looks like so...normalcdf.
The C stands for commulitive which means you add up the numbers as you go along.
For example if you have a group of 4 then another group of 4 and then a last group of 3 you would add them up as so...4...8...11.
The 2nd function that we learned was the probability distribution function. To find this on your calculator you would press 2nd [vars] and it is the first function in the menu.
The P stands for probability which in this case tells a value at a point.
As I was saying earlier that when using the ShadeNorm or the Normalcdf function you will see that you obtain the same answer.
ex. Find the percent of z-scores in a normal standard distribution that are:
a) below z = 0.52
ShadeNorm( -5, 0.52) = 0.6985
Normalcdf( -5, 0.52) = 0.6985
As you can see your answers are the exact same.
Besides dealing with z-scores again and learning a couple of new functions on the calculator we went over the homework questions from last night. I would try to help and explain them myself but even I am having some difficulties with the problems so I apologize for that. I am gonna get some extra help with that so that the next time I do a scribe I can help everyone out 100%. I hope what i have written has helped you all out. The next scribe is......David-san!
Scribe Post
Monday, March 24, 2008
Sunday, March 23, 2008
Scribe Post
On thursday's class we talked more about Z-Scores and how we can enter them into our graphing calculator. We also discussed "how to work with the normal distribution" taking raw data and arranging it in curves. (Seen on slides 4 and 5)


 I hope this helped anyone who was having some trouble following the lesson during last Thursday's class. The next scribe will be..... Grace
I hope this helped anyone who was having some trouble following the lesson during last Thursday's class. The next scribe will be..... GraceThursday, March 20, 2008
Wednesday, March 19, 2008
Scribe Post
Today we had a double class, and on the morning class we had a quiz, which was composed to two questions exactly as they appeared on last night's homework. It was an easy way for Mr. K. to tell who did their homework and who did not. We then went over all the answers in it and how they are marked, so we have a better idea what can hurt you in a test in the future. Remember, SHOW YOUR WORK
After the quiz we started the new lesson for the day, called The Normal Curve. By definition, the Normal Distribution is a frequency distribution that can be represented by a symmetrical bell-shaped curve which shows that most of the data are concentrated around the centre (or the mean) of the distribution.
Remember, normally, data would never fit in the normal perfectly, but there are many situations where the data is approximately normal.
We also learned that the Normal Curve is related to the standard deviation rule mentioned earlier in the course, the 68-95-99 rule, which means that:
Then, for the afternoon class, we were separated into groups and worked on 4 different problems using the normal curve. We had to find out if the data was approximate to the normal distribution or not, and also learned a new way to find it in your calculator... by graphing it!
So, the first way is to find the mean and the standard deviation, by going to 1 variable statistics, or 1-Var Stats, and adding/subtracting the standard deviation to the mean once, twice and three times. Then you turn what you just calculated into percentages, and compare with the 68-95-99 rule. If the percentages are somewhat near 68, 95 and 99, then the data is normal.
The second way, which in my opinion if much easier, is to simply list all the data in your calculator, and graph it by going to stat plot and setting the Xlist to L1 (or whichever list you punched the data in) and the Frequency to 1. Then you would go to zoom and select ZoomStat so the graph fits nicely in your screen.
Well, I guess this about sums it up for what we did today in class, hope my post was of any help. The scribe for tomorrow can be Adamson (bet you wish you didn't give me birthday beats yesterday now haha)
Tuesday, March 18, 2008
Monday, March 17, 2008
Article 13, Al Upton, and the minilegends

You can also read more about Article 13 and the Convention on the Rights of the Child here. This movie illustrates what it's all about:
Scribe Post
We studied about Statistics , there are some definitions we should remember :
_ Statistics : The branch of mathematics that deal with collecting, organizing, displaying, and analyzing data.
_ Datum : one bit (piece) of information.
_ Data : many bits (pieces) of information.
_ Mean : The symbol for mean is "X bar". The arithmetic average of a set of values.
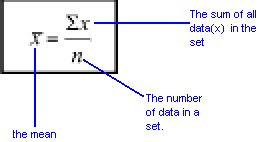
_ Median (med) :
1) The middle value in an ordered (from smallest to largest) set of data.
2) If there are an event number of data, the median is the average of the middle pair in an order of data.
_ Mode : the datum that occurs most frequently in a set of data.
_ Standard Deviation:

Friday, March 14, 2008
Thursday, March 13, 2008
Wednesday, March 12, 2008
Tuesday, March 11, 2008
BOB
BOB
Class was pretty helpful 'today'. I too had trouble deciding whether to use
the combination or permutation formula on certain problems but it is a bit
more clarified now. It can get a little bit tricky but next time I guess I should
just read the question more carefully. And to remember on certain problems
whether to use pick or choose.. maybe I should think that "picking" is
somewhat like favouring a person or a thing when selecting a person onto a
team or whatever (order matters). And "choosing" as the opposite... choosing
people without care of who you choose and what order haha. Well that's
just my interpretation of it. =] Good luck on the test everyone.
BOB- Probability
goodluck dudes!
Monday, March 10, 2008
BOB
Other than that, I think I understand the rest because I'm pretty sure that I'll be able to solve questions that involve independent, dependent events and pathway of counting questions. I also know I'll have to take my time reading questions on the fundamental principal of counting so that I don't rush through it and miss a step. Oh! And questions like A Great Way to Make Money and Give a Worm a Chance were pretty hard questions and hopefully they won't be on the test =) *hint hint.. lol kay thats all..
BOB
SCRIBE
BoB
First of all, the Pre-test today in class seemed pretty easy but I know it's gonna be different tomorrow during the real Test. I'm expecting a harder long answer questions and 4 pages of test papers.
So, now here's my BoB. Well, today we went over some Probability questions from people and the one thing that really helped me alot is the difference between nPr and nCr. I think nPr means, an arrangement of the elements of a set in some order and nCr means a combination is an un-ordered collection of unique elements. So, that's the only thing I'm having trouble with. I'll try to do more exercises to really understand the concept of nCr and nPr. The one thing I truly understand is the Pascal's triangle. It gives me an idea of what to do next by using a pattern.
Well, I guess that's my BOB for this unit which is about Probability. I expect(fingers crossed) to get at least 80% on the test and the probability of me passing is 80/100 which is 8/10 when simplified. And the probability of Applied Mathers doing their BOB is 20/25 which is 4/5 when simplified. That's all and Good Luck Y'all. Ya dig?
BOB
That's why we have 10C4 : number of ways to choose 4 from 10 people, and 2C2 : number of ways to choose Deanne and Peter , 8C2 : number of ways to choose 2 another people for the group from 8 people left. We'll get (2C2*8C2)/10C4 as the result of question a , like Mr.K did.
Hope you guys will do better in the test tomorrow.Good luck
BOB
Sunday, March 9, 2008
BOB!
Anyways, back to my BOB. I thought that the probability unit was challenging for me. Just because out of everything in math .. probability is my weakest unit. For sure, I am going to need alot of extra help and studying to do for the test on tuesday. Hopefully I don't blank out on it :S
I would really like to review on everything we did on probability for tuesday's test, just to make sure i understand what i am doing and to hopefully have a good decent mark on the test.
Homework Mark
-Alvin G.
P formula : the order is important (00 and 00 : difference ==> 2 ways)
C formula : the order is not important (00 and 00 : same ==> 1 way )
That is the difference between C and P , and remember review anything we studied in class....Good luck
Homeworkless
I'm having trouble on the Friday's homework on the last slide. Can anyone please help me?LOL! naatt! Good thing I check the slides everyday. Thanks Mr. K(Kewl) for the easiest homework that you gave us. IT's challenging but easy. I don't know what to type so just keep doing your probability exercises and you will ace the test. Latur Terminator.(Arnold?)
Saturday, March 8, 2008
"HOMEWORK MARK"
Friday, March 7, 2008
Homework comment
So ok, there is my comment on the homework.
Scribe Post
Today in the morning class we quickly went over the homework of two days ago, and then were separated into groups for a workshop (since we are done with the unit). The answers for the homework can be seen on the slides posted by Mr. K.
When we started the workshop we had a simple question, relating to Pascal's triangle.

Keep in mind that the numbers in orange are the total amount of ways of getting from A t C as well as from A to B, passing through point P. The numbers in green are the total amount of ways from C to D and finally the numbers in blue are from D t B. If you multiply all of the results (excluding point P) you will get the total amount of ways to get from A to B, which is 6x2x10 = 120
We handed that in for marks, then were left with harder problems to solve within our group. Whichever group had someone go up on the board with a solution would get points (marks).
We did many of those on the afternoon class as well, so I'll just summarize the ideas here.
"Design an experiment using the random number
function of your calculator to determine the
probability of passing a six-question multiple choice
test if you guess all the answers. Each question has
four answers, and one answer is correct in each case.
How many simulations would seem reasonable? What
is the experimental probability of getting at least 50%
on the test?"
For this problem we had 3 different solutions, that were all close to the real value. You you'd need your randBin function of your calculator for it, with the numbers (6, 1/4, 5) meaning that every result you'll have 5 numbers showing, ranging from 0 through 4, for the 6 questions in the problem.
The question after that we had to remember the difference between Pick formula and the Choose formula, being that the order of the numbers matters for Pick formula (I use the saying P is for picky to remember that)
"A party of eight boys and eight girls are going for a picnic. Six of the party can
ride in one car, and four in another. The rest must walk. (Assume anyone can
drive.)"
For this problem we used the choose formula to solve, since the orders of boys and girls do not matter. Remember that even though we did it in separate steps in class, we will most likely be asked the last question in a test.
Finally we were asked a simple question again:
"Fred is in a class that has 7 boys and 15 girls. The teacher selects partners for
a project by drawing names from a hat. What is the probability that Fred's
partner will be a boy?"
The solution for that was rather easy so I'll just explain what to do. Since Fred himself is one of the 7 boys in his class, there are only 6 other boys that can be his partner, and there are 15 girls, making it a total of 21 possible partners. So, his chance of being teamed up with a boy is 6/21, or 29%.
Well, that's all we did today. Remember to do your BOB posts since our test is on Tuesday. Bring up any questions for Monday's class, which we will use for a pretest.
And... the next scribe is..... *drum roll*
JESSIE. Good luck, haha.
Wednesday, March 5, 2008
Scribe Post
Sorry, I did this all on mspaint and the font looked better
and more readable as a file until it had to be uploaded onto here.
Here are links to the .bmps if you're having trouble reading it on here.
OR just click the pictures on this post.
http://members.shaw.ca/c_macs/1.bmp
http://members.shaw.ca/c_macs/2.bmp
http://members.shaw.ca/c_macs/3.bmp
http://members.shaw.ca/c_macs/4.bmp
http://members.shaw.ca/c_macs/5.bmp
http://members.shaw.ca/c_macs/6.bmp
Sorry again for the inconvenience.






Anyway, that was a lot. I tried though. Hopefully it helps.
I believe this should be worth 2 scribe points! :D
See you...
Oh and.. next scribe will be..
-=''[][][][] . . : : Яέήάή : : . . [][][][]`'=-
haha :)
Tuesday, March 4, 2008
Scribe
We also learned the difference between combinations and permutations.
Permutations are ordered arrangement of objects.
An example of this is license plates
You can have ABC 123, BAC 231 or either CBA 321 …etc.
Although you are using the same letters and numbers, the order they are put in are important because they all represent different license plates.
The formula for permutations is:
And to get this formula plugged into your calculator if you go MATH > PRB > #2
To find the number of combinations, you first calculate the number of permutations the divide by the number of ways a single set could be rearranged.
The formula for combination is:
Anyways thats all..next scribe post will be d[x_x]b
Monday, March 3, 2008
or 7! = 5040 ways
Question b :
In how many ways will the french books are together:
At first we put 3 Fernch books in a bag, and find how many way can arrange this bag and 4 English books, It will = 5!. After that we find how many way 3 french books in the bag can arrange, which is 3! .So...we have 5! to arrange the bag and English books,3! to arrange the frech books in the bag=> the number of way to do both of this is 5! .3! = 720 ways.
Then , we learn the formula n!/(k1*k2*k....)
Where : n total ways to arrange
k the number of way overlap
Ex In the word BOOK , we have total ways to arrange is 4!
and we see 2" O " which could be repeat like this OO and OO
because it is the same word so we don't need it the number of way is 4!/2! = 12 ways
The same with the word MISSISSIPPI = 11!/(4!*4!*2!)= 34650 ways
That is all of the Importance point ( I think ^^)
Bye bye
Sunday, March 2, 2008
QUESTION 1:
We were given the option every week of either $10 or picking two bills out of a bag, which contained two $1 bills, two $5 bills, and a $10 bill. So in the long run which option was better.
-1st we make our tree diagram to show all possibilities of picking 2 bills out of the bag.

So then, once we find the probability of the 1st bill being pulled out, we find the probability of the 2nd bill being pulled out of the bag. To find the probability of 2 bills being pulled out, Multiply the probability of the 1st bill(should be put into fraction) by the probability of the 2nd bill.
ex: first bill is $1, the probability of pulling one dollar is 2 out of 5, because we got 5 bills and 2 of those bills are $1 bills. Lets pretend the 2nd bill is a $1 bill. The probability of pulling another $1 bill after we already pulled out one $1 bill is 1 out of 4. So we multiply the two fractions 2/5 *1/4 = 2/20.

Now if we have 2 numbers that are the same, we just add the fractions together(the denominator does not change).

Now we just find the % of each number possible of pulling out, by dividing the top number by the denominator and Multiply that by 100.
- Now in the long run, which is better? $10 a week or picking 2 bills out of the bag?
For this example we used 100 weeks to make it nice and easy to read.

So basically, there is 10% that you will pull 2 dollars out of the bag. 10% of 100 is 10. take that 10 and multiply it by 2 to get the possibility of getting $20 out of 100 weeks, by pulling two $1 bills. $10 a week is better opposed to only a possibility of $880 in a 100 weeks.
QUESTION 2:

SO the question asked us, how many different 4 digit numbers are there in which all the digits are different. Okay well there are 9 different digits plus 0 that make up the whole number chart.
The question asked us to make 4 digits.
_ _ _ _ = _
1st 2nd 3rd 4th
So in the 1st slot we have 9 different possibilities because we can't use 0. Now on the 2nd slot we have to minus 1 because we used 9, but now we can use 0 so we still have 9 different ways. the 3rd slot we gotta take out the 0 which leaves us with only 8 possibilities. Then we take out 1 more number that we used which leaves us with 7 ways on slot 4. To find the total number of ways of arranging 4 different digits, we multiply each slot by the others.
QUESTION 2 (B)

So now the question asked us how many of those numbers are odd?
-well odd numbers will end in odd. The only odd numbers there is are: 1, 3, 5, 7, and 9.
5 odd numbers. stick 5 at slot 4, so we know it will end with an odd number.
Since we used 1 number at the end, for the 1st slot we minus 1 way which leaves us with 8 ways of arranged a number in slot 1. In slot 2 we can use 0 so that gives us 8 again because we had to abide by the 1st rule ( 4 different digits). then the 3rd slot we have 7 ways. Multiply the slots together and we get our answer.
QUESTION 2 (C)

Now we had to find how many of those numbers are divisible by 5. well with the number ends with 0 or 5 it can be divided by 5.
We had to show 2 diagrams. one with 0 at the end and one with 5 at the end. the concept is the same, but this time once we find our answer for each diagram we add them together to find the real answer.
QUESTION 3.
I didn't really understand this question, so I don't think I can explain it in case I mislead people, but I understand its the same concept as previous questions, with more thinking.
Well hopefully I can understand that question to the point where I can teach it.
--The next scribe is.....................cowmilk