Friday, February 29, 2008
Thursday, February 28, 2008
Wednesday, February 27, 2008
Scribe Post
Warm Up….
Question # 1
Find the probability of flipping three pennies and getting at lest 1 heads.
Ex. 1. Heads AND Heads AND Heads mean multiplied.
2. Heads OR Heads mean add*
Question # 2
How Many Ways
A.) The café special for lunch offers a choice between two main courses (hamburger or chicken burger) and three different drinks. The “meal deal” allow you to pick one each. How many different “meal deal” are there?
“The Fundamental Principal of Counting”
If there are M ways to do a first thing & N ways to do second thing then there are M * N ways to do both things.
Ex. Any one of 4 ties can be matched with any one of 3 shirts, how many shirts & ties combinations are possible?
1.) How many 4 digit #’s are there if the same digit CANNOT be used twice?
* The First # can’t start with 0.
* The same rule applies here can’t start with 0.
Tuesday, February 26, 2008
Scribe Post - Pascal's Triangle
Well the first math class (this morning) we had a pep rally. The beginning of afternoons class we went over last nights homework. Then we went over Pascals Triangle.
We started off with something alittle simple. We went over a number triangle.

- To get this trianle of numbers, you see that all the numbers on the right and left side are all the number 1.
- To get the middle numbers you add the numbers above it. So for the 3rd row you add 1+1=2.
- The 4th row to get the 3's you add 1+2=3.
- The 5th you add 1+3=4 , 3+3=6, 3+1=4
and so on.
We also went over many different ways to find patterns in Pascals Triangle.
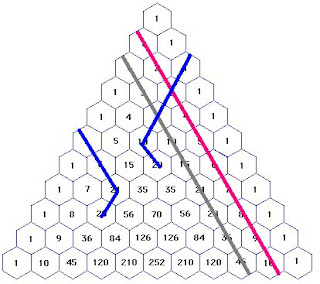
The Pink line is just showing the its the numbers 1-10.
The BLUE Lines represent the "hockey stick".
-When you add 1,3,6, &10 together you get 20.
-When you add 1,6, & 21 together you get 28.
The GREY line is how many "dots" would make a triangle. Example:
< -----
Also, if you put
11^0 = 1
11^1 = 11
11^2 = 121
11^3 = 1,331
11^4 = 14,641
Another way of using Pascal's Triangle is in a word problem. Like this :
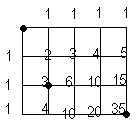
Home = top left corner
School = bottom right corner
and the other is post office.
In that problem it asks how many ways to get to the pst office from home. By using pascal's triangle, we figured that there are 3 ways to get from home to the post office.
ALRIGHTY, well i think thats all, hopefully it helps. (:
Next to scribe is ....... Vanessa
Monday, February 25, 2008
Scribe Post : Probability
Hey guys.. ok so today we worked more on probability specifically theoretical and experimental probability. As a recap:
Experimental Probability is the chance of something happening based on completing an experiment.
Ex: Tossing 3 pennies, using heads to represent boys and tails for girls, then repeating the toss 10 times, representing a family with three children.
Theorectical Probability is the chance of something happening based on realistic circumstances.
Ex.When having a child, there are only two outcomes. Either the child is a girl or boy, therefore there is a 50% chance it will be a girl and 50% chance it will be a boy. For the second child, there are no restrictions as to wether the child will be a girl or boy, so then once again the chance of having a girl remains 50% and for a boy 50% aswell.
Today we learned that we can easily use a tree diagram to help us find outcomes. For example using the example as stated under the theorectical definition:
Remember: inorder for it to be easily followed or understandable, the diagram must be expressed neatly. So if you follow the branches of the tree diagram, you would get outcomes such as:
So if you follow the branches of the tree diagram, you would get outcomes such as:
B B B
B B G
B G B
B G G - exactly 2 girls outcome #1
G B B
G B G - exactly 2 girls outcome #2
G G B - exactly 2 girls outcome #3
G G G
For this example, it asks how many outcomes consist of exactly 2 girls. The answer would be "3 out of 8"
Today we learned how to calculate probability on our TI-83 which we would call stimulating binomial experiments (number of trials, probability of success, number of stimulations). So using the example: In a family of three children, what is the probability that 2 of the children will be girls? We calculated it in class.
So on your TI-83 follow step by step intructions:
1. select [MATH]
2. slide over to [PROB]
3. select [randBin] (random binomial experiment)
4. type in (1, 3/8,40)
- 1 represents the outcome for success.
- 3/8 represents the theorectical probability of success
- 40 represents the # of times the experiement is repeated
5. click [ENTER]
- this will calculate the outcome
- "1" representing successes and "0" representing failures.
Instead of counting the number of time the experiment is successful, it can be calculated throught the calculator, so with #5 of the the steps above still on your screen continue the following:
6. select [STO] [2nd] [L1]
- this will store the information in List 1 (L1)
7. select [2nd] [STAT]
8. select [MATH] slide down to [sum] [2nd] [L1]
- this will calculate of the successes or all the failures.
Like Mr. K said in class informfation such as the information we entered into the calculator: (1, 3/8, 40) you will need to know how to calculate for yourself for test, quizzes and the exam.
ok well think that is it. See ya later!
The Scribe for tomorrow will be Melissa S.
Thursday, February 21, 2008
Scribe Post
hm... Mr. Kuropatwa when you read this can you get back to me please!
BOB
For me specially, i cleared out most of my muddiest points tonight already. All in all, i think that this unit was piece-easy. It took some time for us to get some of the explanation, but in the end we seem to have gotten it through our heads. Study well guys, goodluck to us all!
BOB - Matrices
Wednesday, February 20, 2008
Well the matrices unit was fairly easy except for the transition matrix part and some of the word problems. I know i'm not alone when I say that we had a little bit of difficulty with it. But overall, I was able to work with the other problems smoothly. That's it for now. Good luck on the test tommorow everyone !
Tuesday, February 19, 2008
BOB - Matrices
BOB - MATRICES
GOODLUCK EVERYONE!
BOB-Matries
Till next time bye for now!
February 19 - Introduction to Probability
Im not sure if i am supposed to be the scribe for today since i don't see the last scribes that we're supposed to be posted (unless it's just my computer). But i was told today in class by ickie that i am the next scribe. So just incase, I'll do the scribe for today anyway.
Today we started our second unit which is on Probability.
We learned a variety of language today, with many definitions and some formula's.
Probability: The branch of mathematics that deals with chance.
Sample Space: The set of all possible things that can happen for a given set of circumstances.
ex: Rolling a die 6, .. the sample space would then be {1,2,3,4,5,6}.
Event (E): A subset of the sample space. One particular outcome for a given set of circumstances.
Simple Events: The result of an experimental carried out in 1 step.
Compound Event: The result of an experimental carried out in more than 1 step.
Certain Event: An events whose probability is equal to 1.
Impossible Event: An events whose probability is equal to 0.
Calculating Probability Event:
* The "total number of outcomes" is the sample space.
Probability can be expressed as:
- A ratio
- A decimal
- A fraction
- A percent
**Important: Probability is always a number between 0 and 1!
Complimentary Events:
Is either written as E' or E. The compliment of an event refers to the case where E does not occur.
Ex: H= Drawing a Heart from a deck of 52 cards.
H'(the compliment)= Drawing a card that is not a heart.
Calculating Probability Complimentary:
P(E) + P(E') = 1
so ....
P(E) = 1 - P(E') .... OR .... P(E') = 1 - P(E)
Anyway, I hope that helped you guys alittle bit. If not, there are the slides that Mr. K posted up. Maybe you'll be able to understand it better there.
The next scribe will be christine m.
BOB - Matrices
Friday, February 15, 2008
The Scribe List
This post can be quickly accessed from the [Links] list over there on the right hand sidebar. Check here before you choose a scribe for tomorrow's class when it is your turn to do so.
IMPORTANT: Make sure you label all your Scribe Posts properly or they will not be counted.
Cycle 1
NguyenX SeZy | CJ David-san | ickie (-1) H2O Ari5 |
3.23
Thursday, February 14, 2008
BOB...Matrices
BOB: MATRICES
Wednesday, February 13, 2008
BOB
In this Matrices unit I would have to say that my personal "muddiest point" would be the word problems. Involving what we already know into realistic (sometimes) situations. Most of them are quite simple but there are some that are a bit tricky and confusing at the same time. But usually the tricky questions are the ones that just need to be read over more carefully so I can get it. But good thing we had that review practice at class yesterday, it really did help.
See you all later.
Tuesday, February 12, 2008
BOB
BOB
scribe
So the question that was given to us in class was:
The annual Oxford - Cambridge boat race, has been rowed regularly since 1839. Using data from 1839 up to 1982, there were 57 Oxford wins and 67 Cambridge wins. If the relationship between the results of a given year and the results of the previous year are considered, the following table can be constructed:
Then part A of the question asked us to “convert the ‘number of wins’ to percentages."
Now moving onto part B of the question, which is asking us to find the probability that oxford will win a game this year and the second and third year.
In order to find the probability that Oxford will win this year and the following years, we must construct a state matrix that looks like this:
--The “0” represents the probability Cambridge won't win.
Now that we have both the state matrix and the transition matrix, we can use multiplication to solve part B of the question.
Before I go onto part C, I’ll do part D of the question first because it’s exactly the same as part B. The only difference is that state matrix because now, it looks like this:
Now that we have all the information we need, repeat exactly what we did in Part B to part D. Giving us:
Now going back to part C, the question is asking us “over many years, what percentage of games will Oxford win and Cambridge?”
Since the question isn’t asking for when it stabilizes, I just picked a random number like 50, and multiplied it, like so:
Monday, February 11, 2008
BOB
February 11,2007 - Transition Matrices
- A transition matrix is a square matrix describing the probabilities of moving from one state to another in a dynamic system.
For more info, check out:
http://economics.about.com/library/glossary/bldef-markov-transition-matrix.htm
Example:
In Winnipeg, there is a workforce of 2800 people, with 2500 employed and 800 unemployed. During the course of one year, 20% of the employed workers will lose their jobs and 50% of the unemployed will find jobs.
CLICK THE IMAGE BELOW:
“It isn't that they can't see the
solution.It is that they can't
see the problem.”
-- G. K. Chesterton
Forecast for February 12, 2008(Tuesday)
-11`C with a light snow and a wind of
20km/h.
BTW: Next scribe is YELLOW
Sunday, February 10, 2008
Feb. 08, 2008 (Friday) Connecting Matrices
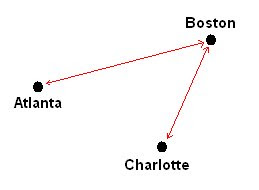 The first problem that we were supose to solve was the flightpaths of Atlanta, Boston and Charlotte.
The first problem that we were supose to solve was the flightpaths of Atlanta, Boston and Charlotte.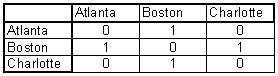 This matrix represents a one hop. Look at the first row first column. The number 1 inticate that there is one route between the city in the row and column for that cell. The 0 indicates that there is no route between the two cities.
This matrix represents a one hop. Look at the first row first column. The number 1 inticate that there is one route between the city in the row and column for that cell. The 0 indicates that there is no route between the two cities.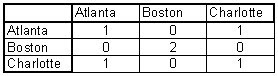
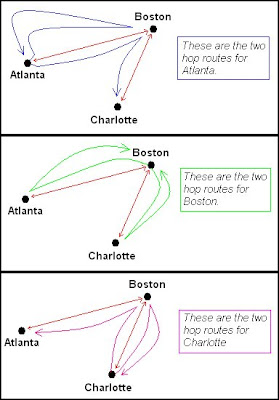
Tip!
Friday, February 8, 2008
Today's Slides and Homework: February 8


Thursday, February 7, 2008
MATRIX MULTIPLICATION
So, we already learned how to add matrices and multiply matrices by scalars. Today we learned how to solve MATRIX MULTIPLICATION.
What is MATRIX MULTIPLICATION?
- it is the operation of multiplying a matrix with either a scalar or other matrix.
Matrix multiplication is not commutative except in special cases.
Commutative law is when numbers can be added or multiplied in any order
Here is how to do it:
We are asked to multiply matrix A and matrix B.
So first, we have to CHECK the DIMENSIONS. If middle numbers aren't matching we cant multiply them. The middle numbers have to be matching to be able to calculate it. If they are not matching it is not possible to calculate it.
Since they both have 2x2 dimension we dont really need to check the middle number.
-You multiply the rows of matrix A by the columns of matrix B.
-Take the first row of A and the first column of B.
-Then, multiply the first entries and the second entries and then add the two products.
-The sum is one entry of the product matrix AB.
-You just do the same thing when you take the second row of A and the second column of B.
Here are other examples that we did in class today:
I hope you find my explanation and examples understandable. If you still have problems in this topic please see http://www.purplemath.com/modules/mtrxmult.htm
The next scribe is Chris29.








